June 6, 2021 25 min to read

[통계계산] 2. LU Decomposition

Computational Statistics

[통계계산] 2. LU Decomposition

목차

Computer Arithmetic

LU decomposition

Cholesky Decomposition

QR Decomposition

Interative Methods

Non-linear Equations

Optimization

Numerical Integration

Random Number Generation

Monte Carlo Integration

sessionInfo()

R version 3.6.3 (2020-02-29)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Ubuntu 18.04.5 LTS

Matrix products: default
BLAS:   /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.7.1
LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.7.1

locale:
 [1] LC_CTYPE=en_US.UTF-8       LC_NUMERIC=C              
 [3] LC_TIME=en_US.UTF-8        LC_COLLATE=en_US.UTF-8    
 [5] LC_MONETARY=en_US.UTF-8    LC_MESSAGES=en_US.UTF-8   
 [7] LC_PAPER=en_US.UTF-8       LC_NAME=C                 
 [9] LC_ADDRESS=C               LC_TELEPHONE=C            
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C       

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

loaded via a namespace (and not attached):
 [1] fansi_0.5.0       digest_0.6.27     utf8_1.2.1        crayon_1.4.1     
 [5] IRdisplay_1.0     repr_1.1.3        lifecycle_1.0.0   jsonlite_1.7.2   
 [9] evaluate_0.14     pillar_1.6.1      rlang_0.4.11      uuid_0.1-4       
[13] vctrs_0.3.8       ellipsis_0.3.2    IRkernel_1.1      tools_3.6.3      
[17] compiler_3.6.3    base64enc_0.1-3   pbdZMQ_0.3-5      htmltools_0.5.1.1

Required R packages

library(Matrix)

Computer methods for solving linear systems of equations

We consider computer algorithms for solving linear equations $\mathbf{A} \mathbf{x} = \mathbf{b}$, a ubiquitous task in statistics.

Our mantra

The form of a mathematical expression and the way the expression should be evaluated in actual practice may be quite different.
– James Gentle, Matrix Algebra, Springer, New York (2007).

Algorithms

Algorithm is loosely defined as a set of instructions for doing something, which terminates in finite time. An algorithm requires input and output.

Measure of algorithm efficiency

A basic unit for measuring algorithmic efficiency is flop.

A flop (floating point operation) consists of a floating point addition, subtraction, multiplication, division, or comparison, and the usually accompanying fetch and store.
How to measure efficiency of an algorithm? Big O notation. If $n$ is the size of a problem, an algorithm has order $O(f(n))$, where the leading term in the number of flops is $c \cdot f(n)$. For example,
- matrix-vector multiplication A * b, where A is $m \times n$ and b is $n \times 1$, takes $2mn$ or $O(mn)$ flops
- matrix-matrix multiplication A * B, where A is $m \times n$ and B is $n \times p$, takes $2mnp$ or $O(mnp)$ flops
Typical orders of computational complexity:
- Exponential order: $O(b^n)$ (“horrible”)
- Polynomial order: $O(n^q)$ (doable)
- $O(n \log n )$ (fast)
- Linear order $O(n)$ (fast)
- Logarithmic order $O(\log n)$ (super fast)
Difference of $O(n^2)$ and $O(n\log n)$ on massive data. Suppose we have a teraflops supercomputer capable of doing $10^{12}$ flops per second. For a problem of size $n=10^{12}$, $O(n \log n)$ algorithm takes about $10^{12} \log (10^{12}) / 10^{12} \approx 27 \text{ seconds}.$ $O(n^2)$ algorithm takes about $10^{12}$ seconds, which is approximately 31710 years!
The QuickSort and Fast Fourier Transform (invented by John Tukey–recall “bit–) are celebrated algorithms that turn $O(n^2)$ operations into $O(n \log n)$.

Triangular systems

Idea: turning original problem into an easy one, e.g., triangular system.

Lower triangular system

To solve $\mathbf{A} \mathbf{x} = \mathbf{b}$, where $\mathbf{A} \in \mathbb{R}^{n \times n}$ is lower triangular

\[\begin{pmatrix} a_{11} & 0 & \cdots & 0 \\ a_{21} & a_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix}.\]

Forward substitution: $\begin{eqnarray*} x_1 &=& b_1 / a_{11} \\ x_2 &=& (b_2 - a_{21} x_1) / a_{22} \\ x_3 &=& (b_3 - a_{31} x_1 - a_{32} x_2) / a_{33} \\ &\vdots& \\ x_n &=& (b_n - a_{n1} x_1 - a_{n2} x_2 - \cdots - a_{n,n-1} x_{n-1}) / a_{nn}. \end{eqnarray*}$
$1 + 3 + 5 + \cdots + (2n-1) = n^2$ flops.
$\mathbf{A}$ can be accessed by row ($ij$ loop) or column ($ji$ loop).

Upper triangular system

To solve $\mathbf{A} \mathbf{x} = \mathbf{b}$, where $\mathbf{A} \in \mathbb{R}^{n \times n}$ is upper triangular
$\begin{pmatrix} a_{11} & \cdots & a_{1,n-1} & a_{1n} \\ \vdots & \ddots & \vdots & \vdots \\ 0 & \cdots & a_{n-1,n-1} & a_{n-1,n} \\ 0 & 0 & 0 & a_{nn} \end{pmatrix} \begin{pmatrix} x_1 \\ \vdots \\ x_{n-1} \\ x_n \end{pmatrix} = \begin{pmatrix} b_1 \\ \vdots \\ b_{n-1} \\ b_n \end{pmatrix}.$

Back substitution (backsolve): $\begin{eqnarray*} x_n &=& b_n / a_{nn} \\ x_{n-1} &=& (b_{n-1} - a_{n-1,n} x_n) / a_{n-1,n-1} \\ x_{n-2} &=& (b_{n-2} - a_{n-2,n-1} x_{n-1} - a_{n-2,n} x_n) / a_{n-2,n-2} \\ &\vdots& \\ x_1 &=& (b_1 - a_{12} x_2 - a_{13} x_3 - \cdots - a_{1,n} x_{n}) / a_{11}. \end{eqnarray*}$
$n^2$ flops.
$\mathbf{A}$ can be accessed by row (ij loop) or column (ji loop).

Implementation

Most numerical computing software packages (including R) are built on top of the BLAS (basic linear algebra subprograms).
- Netlib provides a reference implementation.
- Vanila R (the binary that you can download from https://www.r-project.org) uses its own implementation of BLAS (see sessionInfo() above)

The BLAS triangular system solve is done in place, i.e., $\mathbf{b}$ is overwritten by $\mathbf{x}$.

  # forward substitution
  for (i in seq_len(n)) {
      for (j in seq_len(i-1)) {
          b[i] <- b[i] - A[i, j] * b[j]
      }
      b[i] <- b[i] / A[i, i]
  }
  # backsolve
  for (i in rev(seq_len(n))) {
      for (j in i + seq_len(max(n - i, 0))) {
          b[i] <- b[i] - A[i, j] * b[j]
      }
      b[i] <- b[i] / A[i, i]
  }

R
- ?backsolve, ?forwardsolve
- This is a wrapper for the level-3 BLAS routine dtrsm
- The d stands for double precision.

set.seed(123) # seed
n <- 5
A <- Matrix(rnorm(n * n), nrow = n)
b <- rnorm(n)
# a random matrix
A

5 x 5 Matrix of class "dgeMatrix"
            [,1]       [,2]       [,3]       [,4]       [,5]
[1,] -0.56047565  1.7150650  1.2240818  1.7869131 -1.0678237
[2,] -0.23017749  0.4609162  0.3598138  0.4978505 -0.2179749
[3,]  1.55870831 -1.2650612  0.4007715 -1.9666172 -1.0260044
[4,]  0.07050839 -0.6868529  0.1106827  0.7013559 -0.7288912
[5,]  0.12928774 -0.4456620 -0.5558411 -0.4727914 -0.6250393

Al <- lower.tri(A) # Returns a matrix of logicals the same size of a given matrix with entries TRUE in the lower triangle
Aupper <- A
Aupper[Al] <- 0
Aupper

5 x 5 Matrix of class "dgeMatrix"
           [,1]      [,2]      [,3]       [,4]       [,5]
[1,] -0.5604756 1.7150650 1.2240818  1.7869131 -1.0678237
[2,]  0.0000000 0.4609162 0.3598138  0.4978505 -0.2179749
[3,]  0.0000000 0.0000000 0.4007715 -1.9666172 -1.0260044
[4,]  0.0000000 0.0000000 0.0000000  0.7013559 -0.7288912
[5,]  0.0000000 0.0000000 0.0000000  0.0000000 -0.6250393

backsolve(Aupper, b) 

Some algebraic facts of triangular system

Eigenvalues of a triangular matrix $\mathbf{A}$ are diagonal entries $\lambda_i = a_{ii}$.
Determinant $\det(\mathbf{A}) = \prod_i a_{ii}$.
The product of two upper (lower) triangular matrices is upper (lower) triangular.
The inverse of an upper (lower) triangular matrix is upper (lower) triangular.
The product of two unit upper (lower) triangular matrices is unit upper (lower) triangular.
The inverse of a unit upper (lower) triangular matrix is unit upper (lower) triangular.

Gaussian Elimination and LU Decomposition

A toy example.
History: the method is named after Carl Friedrich Gauss (1777–1855), although it stems from the notes of Isaac Newton. If fact, GE was known to Chinese mathematicians as early as 179 AD.

A <- t(Matrix(c(2.0, -4.0, 2.0, 4.0, -9.0, 7.0, 2.0, 1.0, 3.0), ncol=3))  # R used column major ordering
A

3 x 3 Matrix of class "dgeMatrix"
     [,1] [,2] [,3]
[1,]    2   -4    2
[2,]    4   -9    7
[3,]    2    1    3

b <- c(6.0, 20.0, 14.0)

# R's way tp solve linear equation

solve(A, b)

3 x 1 Matrix of class "dgeMatrix"
     [,1]
[1,]    2
[2,]    1
[3,]    3

What happens when we call solve(A, b)?

Elementary operator matrix

Elementary operator matrix is the identity matrix with the 0 in position $(j,k)$ replaced by $c$ $\mathbf{E}_{jk}(c) = \begin{pmatrix} 1 & & \\ & \ddots & \\ & & 1 & \\ & & & \ddots & \\ & & c & & 1 & \\ & & & & & \ddots \\ & & & & & & 1 \end{pmatrix} = \mathbf{I} + c \mathbf{e}_j \mathbf{e}_k^T.$
$\mathbf{E}_{jk}(c)$ is unit triangular, full rank, and its inverse is $\mathbf{E}_{jk}^{-1}(c) = \mathbf{E}_{jk}(-c).$
$\mathbf{E}{jk}(c)$ left-multiplies an $n \times m$ matrix $\mathbf{X}$ effectively replace its $j$-th row $\mathbf{x}{j\cdot}$ by $c \mathbf{x}{k \cdot} + \mathbf{x}{j \cdot}$

\[\mathbf{E}_{jk}(c) \times \mathbf{X} = \mathbf{E}_{jk}(c) \times \begin{pmatrix} & & \\ \cdots & \mathbf{x}_{k\cdot} & \cdots \\ & & \\ \cdots & \mathbf{x}_{j\cdot} & \cdots \\ & & \end{pmatrix} = \begin{pmatrix} & & \\ \cdots & \mathbf{x}_{k\cdot} & \cdots \\ & & \\ \cdots & c \mathbf{x}_{k\cdot} + \mathbf{x}_{j\cdot} & \cdots \\ & & \end{pmatrix}.\]

$2m$ flops (why?).

Gaussian elimination applies a sequence of elementary operator matrices to transform the linear system $\mathbf{A} \mathbf{x} = \mathbf{b}$ to an upper triangular system $\begin{eqnarray*} \mathbf{E}_{n,n-1}(c_{n,n-1}) \cdots \mathbf{E}_{21}(c_{21}) \mathbf{A} \mathbf{x} &=& \mathbf{E}_{n,n-1}(c_{n,n-1}) \cdots \mathbf{E}_{21}(c_{21}) \mathbf{b} \\ \mathbf{U} \mathbf{x} &=& \mathbf{b}_{\text{new}}. \end{eqnarray*}$
Let’s get back to our toy example.

Column 1:

E21 <- t(Matrix(c(1.0, 0.0, 0.0, -2.0, 1.0, 0.0, 0.0, 0.0, 1.0), nrow=3))  # Step 1, inv(L1)
E21

3 x 3 sparse Matrix of class "dtCMatrix"
           
[1,]  1 . .
[2,] -2 1 .
[3,]  . . 1

# zero (2, 1) entry   
E21 %*% A   # Step 1, A'

3 x 3 Matrix of class "dgeMatrix"
     [,1] [,2] [,3]
[1,]    2   -4    2
[2,]    0   -1    3
[3,]    2    1    3

E31 <- t(Matrix(c(1.0, 0.0, 0.0, 0.0, 1.0, 0.0, -1.0, 0.0, 1.0), nrow=3))  # Step 2, find the corresponding matrix!
E31

3 x 3 sparse Matrix of class "dtCMatrix"
           
[1,]  1 . .
[2,]  . 1 .
[3,] -1 . 1

# zero (3, 1) entry    
E31 %*% E21 %*% A  # Step2, A''

3 x 3 Matrix of class "dgeMatrix"
     [,1] [,2] [,3]
[1,]    2   -4    2
[2,]    0   -1    3
[3,]    0    5    1


Column 2:

E32 <- t(Matrix(c(1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 5.0, 1.0), nrow=3))  # Step 3, find the corresponding matrix!
E32

3 x 3 sparse Matrix of class "dtCMatrix"
          
[1,] 1 . .
[2,] . 1 .
[3,] . 5 1

# zero (3, 2) entry
E32 %*% E31 %*% E21 %*% A   # Step 3, A'''

3 x 3 Matrix of class "dgeMatrix"
     [,1] [,2] [,3]
[1,]    2   -4    2
[2,]    0   -1    3
[3,]    0    0   16

Thus we have arrived at an upper triangular matrix $\mathbf{U}$.

Gauss transformations

For the first column, $\mathbf{M}_1 = \mathbf{E}_{n1}(c_{n1}) \cdots \mathbf{E}_{31}(c_{31}) \mathbf{E}_{21}(c_{21}) = \begin{pmatrix} 1 & \\ c_{21} & \\ & \ddots & \\ c_{n1} & & 1 \end{pmatrix}$
For the $k$-th column, $\mathbf{M}_k = \mathbf{E}_{nk}(c_{nk}) \cdots \mathbf{E}_{k+1,k}(c_{k+1,k}) = \begin{pmatrix} 1 & \\ & \ddots \\ & & 1 & \\ & & c_{k+1,k} & 1\\ & & \vdots & & \ddots \\ & & c_{n,k} & & & 1 \end{pmatrix}.$
$\mathbf{M}1, \ldots, \mathbf{M}{n-1}$ are called the Gauss transformations.

M1 <- E31  # inv(L2)
M1

3 x 3 sparse Matrix of class "dtCMatrix"
           
[1,]  1 . .
[2,]  . 1 .
[3,] -1 . 1

M2 <- E32  # inv(L3)
M2

3 x 3 sparse Matrix of class "dtCMatrix"
          
[1,] 1 . .
[2,] . 1 .
[3,] . 5 1

Gauss transformations $\mathbf{M}_k$ are unit triangular, full rank, with inverse $\mathbf{M}_k^{-1} = \mathbf{E}_{k+1,k}^{-1}(c_{k+1,k}) \cdots \mathbf{E}_{nk}^{-1}(c_{nk}) = \begin{pmatrix} 1 & \\ & \ddots \\ & & 1 & \\ & & - c_{k+1,k}\\ & & \vdots & & \ddots \\ & & - c_{n,k} & & & 1 \end{pmatrix}.$

solve(M1)   # L2; solve(A) gives the inverse of A, but use it with caution (see below)

3 x 3 sparse Matrix of class "dtCMatrix"
          
[1,] 1 . .
[2,] . 1 .
[3,] 1 . 1

solve(M2)   # L3

3 x 3 sparse Matrix of class "dtCMatrix"
           
[1,] 1  . .
[2,] .  1 .
[3,] . -5 1

LU decomposition

Gaussian elimination does $\mathbf{M}_{n-1} \cdots \mathbf{M}_1 \mathbf{A} = \mathbf{U}.$
Let

\begin{equation} \mathbf{L} = \mathbf{M}_1^{-1} \cdots \mathbf{M}_{n-1}^{-1} = \begin{pmatrix}
1 & & & &
- c_{21} & \ddots & & &
& & 1 & &
- c_{k+1,1} & & - c_{k+1,k} & &
& & \vdots & & \ddots
- c_{n1} & & - c_{nk} & & & 1 \end{pmatrix}. \end{equation} Thus we have the LU decomposition $\mathbf{A} = \mathbf{L} \mathbf{U},$ where $\mathbf{L}$ is unit lower triangular and $\mathbf{U}$ is upper triangular.

LU decomposition exists if the principal sub-matrix $\mathbf{A}[1:k, 1:k]$ is non-singular for $k=1,\ldots,n-1$.
If the LU decomposition exists and $\mathbf{A}$ is non-singular, then the LU decmpositon is unique and $\det(\mathbf{A}) = \det(\mathbf{L}) \det(\mathbf{U}) = \prod_{k=1}^n u_{kk}.$
- This is basically how R (and MATLAB and Julia) compute determinants.

The whole LU algorithm is done in place, i.e., $\mathbf{A}$ is overwritten by $\mathbf{L}$ and $\mathbf{U}$.

for (k in seq_len(n-1)) {
  for (i in k +seq_len(max(n - k, 0))) {
      A[i, k] <- A[i, k] / A[k, k]
      for (j in k +seq_len(max(n - k, 0))) {
          A[i, j] <- A[i, j] - A[i, k] * A[k, j]
      }
  }
}

The LU decomposition costs $2(n-1)^2 + 2(n-2)^2 + \cdots + 2 \cdot 1^2 \approx \frac 23 n^3 \quad \text{flops}.$

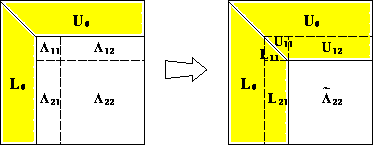
Source: http://www.netlib.org

Actual implementations can differ: outer product LU ($kij$ loop), block outer product LU (higher level-3 fraction), Crout’s algorithm ($jki$ loop).
Given LU decomposition $\mathbf{A} = \mathbf{L} \mathbf{U}$, solving $(\mathbf{L} \mathbf{U}) \mathbf{x} = \mathbf{b}$ for one right hand side costs $2n^2$ flops:
- One forward substitution ($n^2$ flops) to solve $\mathbf{L} \mathbf{y} = \mathbf{b}$
- One back substitution ($n^2$ flops) to solve $\mathbf{U} \mathbf{x} = \mathbf{y}$
Therefore to solve $\mathbf{A} \mathbf{x} = \mathbf{b}$ via LU, we need a total of $\frac 23 n^3 + 2n^2 \quad \text{flops}.$
If there are multiple right hand sides, LU only needs to be done once.

Matrix inversion

For matrix inversion, there are $n$ right hand sides $\mathbf{e}_1, \ldots, \mathbf{e}_n$. Taking advantage of 0s reduces $2n^3$ flops to $\frac 43 n^3$ flops. So matrix inversion via LU costs $\frac 23 n^3 + \frac 43 n^3 = 2n^3 \quad \text{flops}.$
No inversion mentality:

Whenever we see matrix inverse, we should think in terms of solving linear equations. In short, no solve(A) %*% b, but solve(A, b).

We do not compute matrix inverse unless
1. it is necessary to compute standard errors
2. number of right hand sides is much larger than $n$
3. $n$ is small

Pivoting

Let $\mathbf{A} = \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix}.$ Is there a solution to $\mathbf{A} \mathbf{x} = \mathbf{b}$ for an arbitrary $\mathbf{b}$? Does GE/LU work for $\mathbf{A}$?
What if, during LU procedure, the pivot $a_{kk}$ is 0 or nearly 0 due to underflow?
Example: $\begin{split} 0.001x_1 + x_2 &= 1 \\ x_1 + x_2 &= 2 \end{split}$ with solution

\[\begin{bmatrix} x_1 \\ x_ 2 \end{bmatrix} = \begin{bmatrix} 1.001001 \\ 0.998999 \end{bmatrix} \approx \begin{bmatrix} 1.0 \\ 1.0 \end{bmatrix} .\]

With two significant digits, GE via LU yields $\begin{split} 0.001x_1 + x_2 &= 1 \\ (1-1000)x_2 &= 2 - 1000 \end{split}$ or
$\begin{split} 0.001x_1 + x_2 &= 1 \\ -1000 x_2 &= -1000 \end{split} ,$ yielding $\begin{bmatrix} x_1 \\ x_ 2 \end{bmatrix} = \begin{bmatrix} 0.0 \\ 1.0 \end{bmatrix} !$

The condition number of matrix $\mathbf{A} = \begin{bmatrix} 0.001 & 1 \ 1 & 1 \end{bmatrix}$ is 2.262, so the problem itself is well-conditioned: a small change in $\mathbf{A}$ won’t yield a large change in the solution $\mathbf{x} = \mathbf{A}^{-1}\mathbf{b}$. It is the characteristic of the algorithm that yields the large error between the true solution $\mathbf{x}\approx(1, 1)$ and the computed solution (or the output of the algorithm) $\hat{\mathbf{x}}=(0, 1)$. This example suggests that with GE/LU, the worst-case relative error $|\mathbf{x}-\hat{\mathbf{x}}| / |\mathbf{x}| \ge 1/\sqrt{2}$, not small.

The root cause is the vastly different scale of $a_{11}$ with other coefficients and the order of ellimination. In particular, any $a_{22}$ such that $[a_{22} - 1000] = -1000$ will yield the same solution $\hat{\mathbf{x}}=(0, 1)$. (Recall Scenario 1 of Catastrophic Cancellation in Lecture 1.) The $1000 = a_{22}/a_{11}$ causes the loss of information in $a_{22}$ and $b_2$.

Indeed, the LU decomposition of $\mathbf{A}$ within the precision is

$\mathbf{L} = \begin{bmatrix} 1 & 0 \\ 1000 & 1 \end{bmatrix}, \quad \mathbf{U} = \begin{bmatrix} 0.001 & 1 \\ 0 & -1000 \end{bmatrix},$ resulting in $\mathbf{L}\mathbf{U} = \begin{bmatrix} 0.001 & 1 \ 1 & 0 \end{bmatrix}$, and $|\mathbf{A}-\mathbf{L}\mathbf{U}| = 1 \approx |\mathbf{A}|=1.62$.

Solution: fix the algorithm by pivoting.

\[\begin{split} x_1 + x_2 &= 2 \\ 0.001x_1 + x_2 &= 1 \end{split}\]

With two significant digits, GE yields

$\begin{split} x_1 + x_2 &= 2 \\ (1-0.001)x_2 &= 1 - 0.002 \end{split}$ or $\begin{split} x_1 + x_2 &= 2 \\ 1.0 x_2 &= 1.0 \end{split} ,$ yielding $\begin{bmatrix} x_1 \\ x_ 2 \end{bmatrix} = \begin{bmatrix} 1.0 \\ 1.0 \end{bmatrix} .$

Note that $0.001=a_{11}/a_{22}$ does not cause a loss of information in $a_{12}$ and $b_1$. The LU decomposition within the precision is $\mathbf{L} = \begin{bmatrix} 1 & 0 \\ 0.001 & 1 \end{bmatrix}, \quad \mathbf{U} = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}, \quad \mathbf{L}\mathbf{U} = \begin{bmatrix} 1 & 1 \\ 0.001 & 1.0 \end{bmatrix}.$

Partial pivoting: before zeroing the $k$-th column, move the row with $\max_{i=k}^n a_{ik} $ is into the $k$-th row (called GEPP).
- Cost: $(n-1) + (n-2) + \dotsb + 1 = O(n^2)$.
LU with partial pivoting yields $\mathbf{P} \mathbf{A} = \mathbf{L} \mathbf{U},$ where $\mathbf{P}$ is a permutation matrix, $\mathbf{L}$ is unit lower triangular with $|\ell_{ij}| \le 1$, and $\mathbf{U}$ is upper triangular.
Complete pivoting (GECP): do both row and column interchanges so that the largest entry in the sub matrix A[k:n, k:n] is permuted to the $(k,k)$-th entry. This yields the decomposition $\mathbf{P} \mathbf{A} \mathbf{Q} = \mathbf{L} \mathbf{U},$ where $|\ell_{ij}| \le 1$.

GEPP is the most commonly used methods for solving general linear systems. GECP is more stable but costs more computation. Partial pivoting is stable most of times (which is partially because GEPP guarantees $

\ell_{ij}

\le 1$).

Implementation

Except for the iterative methods, most of these numerical linear algebra tasks are implemented in the BLAS and LAPACK libraries. LAPACK is built on top of BLAS. They form the building blocks of most statistical computing tasks.

LAPACK (Linear Algebra Package) is a standard software library for numerical linear algebra. It provides routines for solving systems of linear equations and linear least squares, eigenvalue problems, and singular value decomposition. -Wikipedia

LAPACK routine GETRF does $\mathbf{P} \mathbf{A} = \mathbf{L} \mathbf{U}$ (LU decomposition with partial pivoting) in place.
R: solve() implicitly performs LU decomposition (wrapper of LAPACK routine DGESV). solve() allows specifying a single or multiple right hand sides. If none, it computes the matrix inverse. The matrix package contains lu() function that outputs L, U, and pivot.

A  # just to recall

3 x 3 Matrix of class "dgeMatrix"
     [,1] [,2] [,3]
[1,]    2   -4    2
[2,]    4   -9    7
[3,]    2    1    3

# second argument indicates partial pivoting (default) or not
alu <- Matrix::lu(A)
class(alu)

‘denseLU’

ealu <- expand(alu)

ealu$L

3 x 3 Matrix of class "dtrMatrix" (unitriangular)
     [,1]       [,2]       [,3]      
[1,] 1.00000000          .          .
[2,] 0.50000000 1.00000000          .
[3,] 0.50000000 0.09090909 1.00000000

ealu$U

3 x 3 Matrix of class "dtrMatrix"
     [,1]      [,2]      [,3]     
[1,]  4.000000 -9.000000  7.000000
[2,]         .  5.500000 -0.500000
[3,]         .         . -1.454545

ealu$P

3 x 3 sparse Matrix of class "pMatrix"
          
[1,] . . |
[2,] | . .
[3,] . | .

with(ealu, L %*% U)

3 x 3 Matrix of class "dgeMatrix"
     [,1] [,2] [,3]
[1,]    4   -9    7
[2,]    2    1    3
[3,]    2   -4    2

with(ealu, P %*% L %*% U)

3 x 3 Matrix of class "dgeMatrix"
     [,1] [,2] [,3]
[1,]    2   -4    2
[2,]    4   -9    7
[3,]    2    1    3

det(A) # this does LU!

-32

det(ealu$U) # this is cheap

-32

solve(A) # this does LU!

3 x 3 Matrix of class "dgeMatrix"
        [,1]    [,2]   [,3]
[1,]  1.0625 -0.4375 0.3125
[2,] -0.0625 -0.0625 0.1875
[3,] -0.6875  0.3125 0.0625

with(ealu, solve(U) %*% solve(L) %*% t(P) ) # this is cheap???

3 x 3 Matrix of class "dgeMatrix"
        [,1]    [,2]   [,3]
[1,]  1.0625 -0.4375 0.3125
[2,] -0.0625 -0.0625 0.1875
[3,] -0.6875  0.3125 0.0625

YeonghyeonKO v3.1.0

[통계계산] 2. LU Decomposition

[통계계산] 2. LU Decomposition

목차

Required R packages

Computer methods for solving linear systems of equations

Our mantra

Algorithms

Measure of algorithm efficiency

Triangular systems

Lower triangular system

Upper triangular system

Implementation

Some algebraic facts of triangular system

Gaussian Elimination and LU Decomposition

Elementary operator matrix

Gauss transformations

LU decomposition

Matrix inversion

Pivoting

Implementation

[통계계산] 3. Cholesky Decomposition

Comments

[통계계산] 2. LU Decomposition

[통계계산] 2. LU Decomposition

목차

Required R packages

Computer methods for solving linear systems of equations

Our mantra

Algorithms

Measure of algorithm efficiency

Triangular systems

Lower triangular system

Upper triangular system

Implementation

Some algebraic facts of triangular system

Gaussian Elimination and LU Decomposition

Elementary operator matrix

Gauss transformations

LU decomposition

Matrix inversion

Pivoting

Implementation

[통계계산] 3. Cholesky Decomposition

Share

Comments