July 2, 2020 2 min to read

[회귀분석] 1. 단순선형회귀

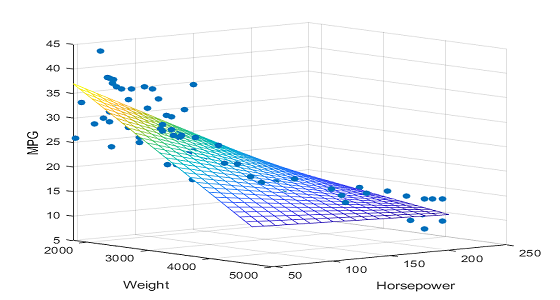
Linear Regression

목차

1. Simple Linear Regression
2. Multiple Linear Regression
3. Model Adequacy Checking
4. Transformation and Weighting
5. Diagnostics for Leverage and Influence
6. Polynomial Regression Models
7. Indicator Variables
8. Multicollinearity
9. Variable Selection
10. Non-linear Regression
11. Generalized Linear Models

1. Review

Probability Distributions
① : Normal Distribution

• $X \sim N(\mu, \sigma^2) \;:\;f_X(x) = \frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{1}{2\sigma^2}(x-\mu)^2}$
  
• $Z \sim N(0, 1) \;:\;f_Z(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}$
  
  

② : Chi-square Distribution

• $V \sim \chi^2(r) \;:\; f_V(x) = \frac{x^{\frac{r}{2}-1}e^{-x/2}}{\Gamma(2/r)2^{r/2}}I_{(x \geq0)}$

  $V = Z_1^2 + \cdots Z_r^2 \sim \chi^2(r)$
  

③ : T Distribution

• $T \sim t(r) \;:\; f_T(x) = \frac{\Gamma(\frac{r+1}{2})}{\Gamma(r/2)\Gamma(1/2)\sqrt{r}}(1+x^2/r)^{-\frac{r+1}{2}}$
  

  $T = \frac{Z}{\sqrt{V/r}} \sim t(r)$
  

④ : F Distribution

• $F \sim F(r_1, r_2) \;:\; f_F(x) = \frac{\Gamma(\frac{r_1 + r_2}{2})}{\Gamma(\frac{r_1}{2})\Gamma(\frac{r_2}{2})}(\frac{r_1}{r_2})^{r_1/2}x^{r_1/2-1}(1 + \frac{r_1}{r_2}x)^{-\frac{r_1+r_2}{2}}$
  

  $F = \frac{V_1/r_1}{V_2/r_2}$

Statistical Estimation
① Unbiasedness : $E(\hat{\theta_n}) = \theta$
② Consistency : $\lim_{n \to \infty} P(|\hat{\theta_n}-\theta| \geq \epsilon) = 0 \;\; for \; \forall \;\epsilon >0$
③ Efficiency : $Var(\hat{\theta_n}) \leq Var(\tilde{\theta_n}) \;\; for \; \forall \;\ \tilde{\theta_n} >0$

Matrix

• Symmetric Matrix :
  $A = A’ = \begin{pmatrix} 1 & 2 & 3\\
  a & b & c\\
  ㄱ & ㄴ & ㄷ \end{pmatrix} = \begin{pmatrix} 1 & a & ㄱ \\\ 2 & b & ㄴ \\\ 3 & c & ㄷ\end{pmatrix}$

• Orthogonal Matrix :
  $AA’ = A’A=I \iff A^{-1} = A’$
  
  

• Idempotent Matrix :
  $AA = A$ (projection matrix)
  
  

• Trace of a Matrix :
  $tr(A) = \sum_{i=1}^k a_{ii}$
  
  

• Quadratic form :
  $y’Ay = \sum_{i=1}^k \sum_{j=1}^k a_{ij}y_i y_j$
  
  

• Expectation and Variance of a Matrix :
  $y_{(k,1)}의 \;평균이 \; \mu, \;분산이 \;V일 \;때,$
  – $E(Ay) = A\mu$
  – $Var(Ay) = AVA’$
  – $E(y’Ay) = tr(AV) + \mu’ A \mu$

2. Simple Linear Regression

Model

• $y = \beta_0 + \beta_1 x + \epsilon$
  ($\epsilon \sim INDEP(0, \sigma^2)$ 가정)
  

• With the error assumption,
  $E(y|x) = \beta_0 + \beta_1 x, \;\; Var(y|x) = \sigma^2$

Least-Square Estimation

• LSE(최소자승법)의 목표는 error를 최소화하는 것.
  

$\iff Minimize \;\;S(\beta_0, \beta_1) = \sum_{i=1}^n (y_i - \beta_0 - \beta_1 x)^2 = \sum_{i=1}^n \epsilon_i^2$
$\iff ① : \frac{\partial S}{\partial \beta_0}|{\hat{\beta_0}, \hat{\beta_1}} = -2\sum{i=0}^n (y_i-\hat{\beta_0} - \hat{\beta_1}x_i) =0 \\
② : \frac{\partial S}{\partial \beta_1}|{\hat{\beta_0}, \hat{\beta_1}} = -2\sum{i=0}^n (y_i-\hat{\beta_0} - \hat{\beta_1}x_i)x_i =0 $

$\iff \hat{\beta_0} = \bar{y} - \hat{\beta_1}x_1 \\
\hat{\beta_1} = S_{xy}/S_{xx}$

(참고문헌)

1. Montgomery 외, 『Introduction to Linear Regression Analysis』, Wiley