1 min to read
[Bayesian] Bayesian Deep Learning - (2) Gaussian Process
Statistics, Gaussian Process, BNN, Bayesian Deep Learning
[Bayesian] Bayesian Deep Learning - (2) Gaussian Process
1. Gaussian Process and Weight Space View

-
Gaussian Process를 이해하기 위해서는 다변량 정규분포(MVN)에 대한 지식이 필요하다. MVN을 따르는 확률변수의 어떤 부분집합에 대해 주변 분포와 조건부 분포 모두 정규분포를 따르는 성질에 더해 GP는 MVN을 무한 차원으로 확장시키는 함수에 대한 분포다. 평균 함수와 공분산 함수를 통해 정의되는 GP에서 중요한 성질 중 하나는
Marginalization Property다. 관측되지 않은 수많은 변수 또는 우리가 관심 없는 변수를 Marginalize할 수 있다. -
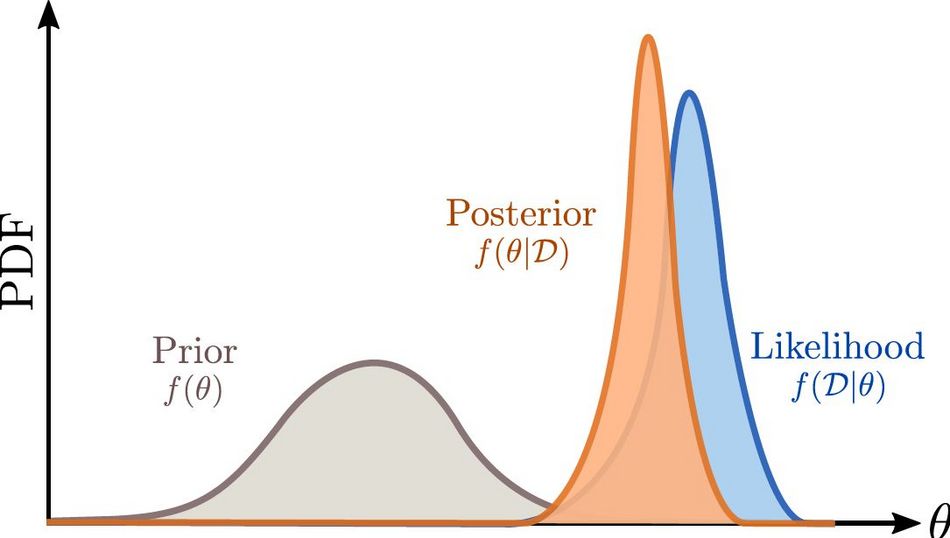
함수에 대한 분포로 정의되는 Gaussian Process는 Bayesian Inference의 Prior로 사용된다. training data가 주어졌을 때 이 Prior를 업데이트하여 새로운 데이터가 주어졌을 때 적절한 예측 값을 반환하는 것이 후술할 Posterior Gaussian Process의 목표다.
-
training data의 분포를 $f$로, 새로운 데이터를 $f \ast$로 정의하여 다음과 같은 결합 분포를 상정하자.
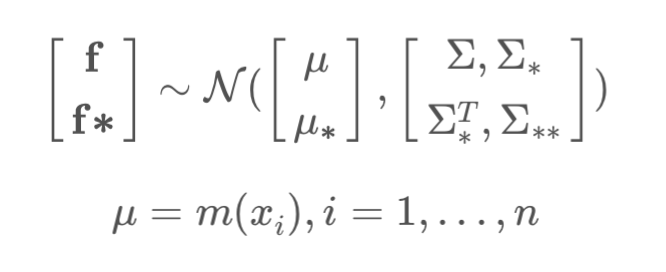
- 이때, 우리가 찾고 싶은 $f \ast$ 의 조건부 분포는 결합 정규분포를 조건화하는 공식에 따라 $f \ast \rvert f ~ N(\mu \ast + \Sigma \ast^T \Sigma^{-1} (f - \mu), \; \Sigma \ast \ast - \Sigma \ast^T \Sigma^{-1} \Sigma \ast)$ 과 같이 주어진다.
2. Function Space View

3. Guassian Process Latent Variable Model


참고자료
- 최성준, Bayesian Deep Learning
- https://greeksharifa.github.io/bayesian_statistics/2020/07/12/Gaussian-Process/
Comments